Estimating a Physician's Schedule using a Binomial Distribution
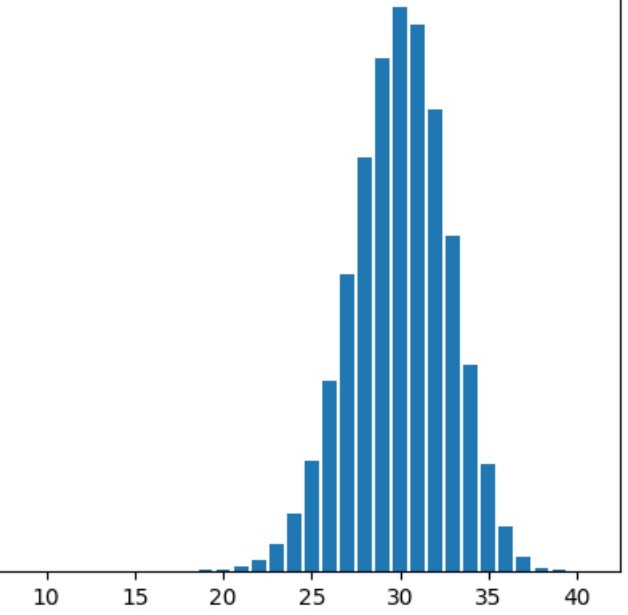
- The objective of this project is to estimate the number of appointments a physician should schedule in order to maximize the number of patients given 25% of patients will not show up in a python jupyter notebook.
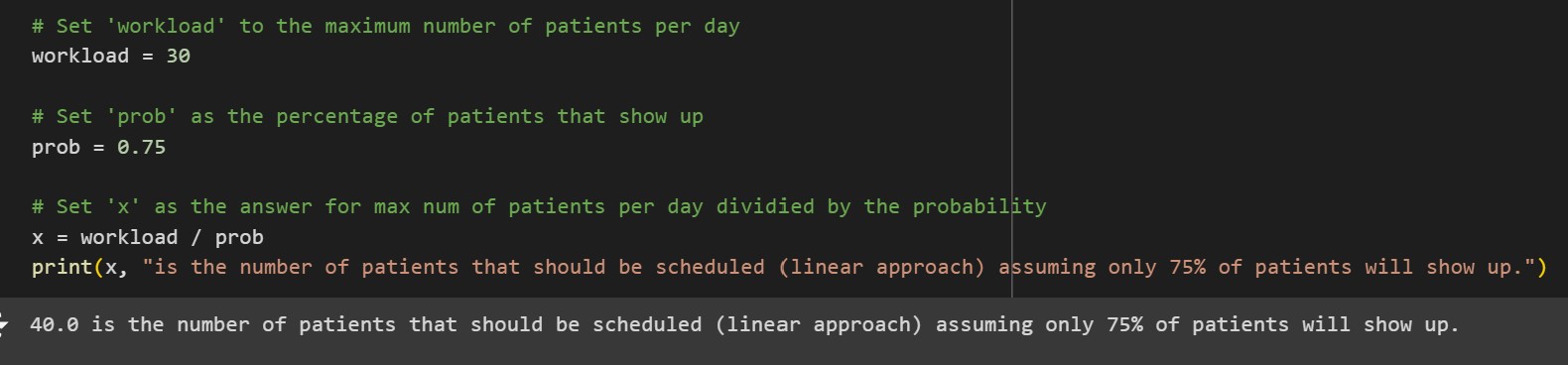
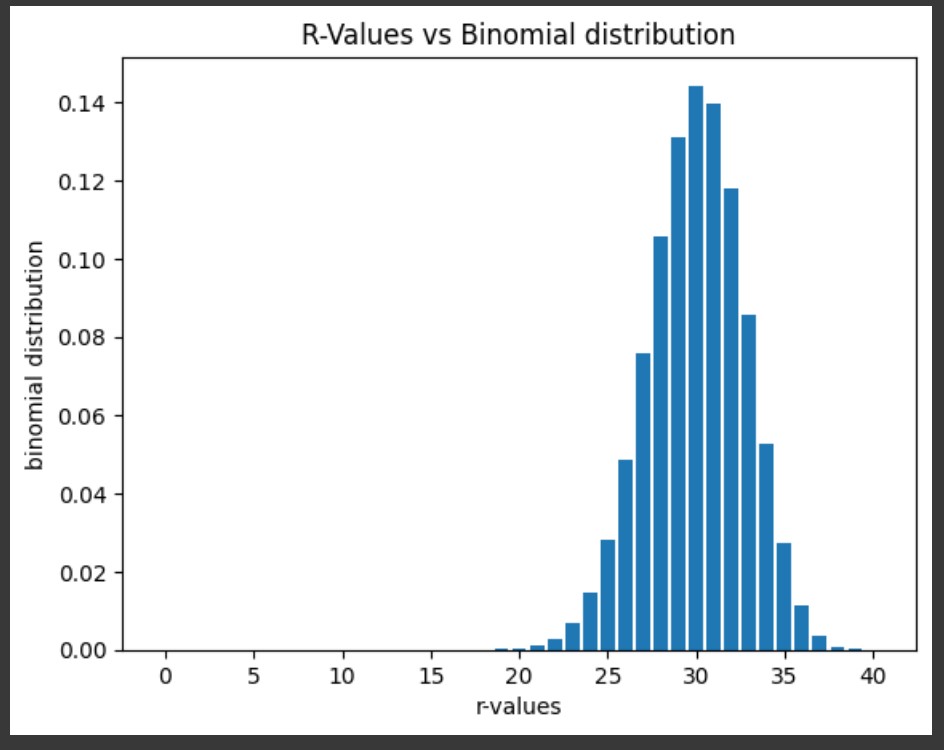
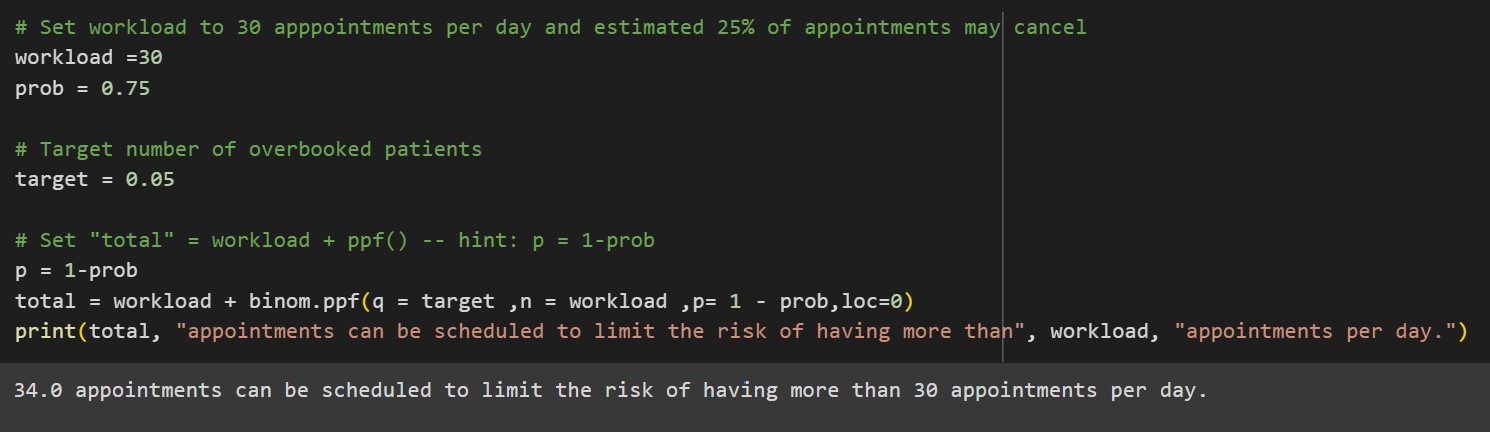
- The exercise first considers a linear approach, followed by a binomial distribution in order to maximize the number of appointments. The number of patients that should be scheduled considers the physician can see a maximum of 30 patients per day and the probability that a patients will show up is 75%.
- Tables and graphs can be found here: Estimating a Physician's Schedule using a Binomial Distribution Python Jupyter Notebook (8/12/2024 Update)